Qu’appelle-t-on l’altitude d’un point ?

Qu’appelle-t-on l’altitude d’un point ? En juillet 2025, j’ai réalisé que je ne m’étais jamais vraiment posé cette question. Bien sûr, comme vous, je suis allé à l’école et, comme vous, j’ai appris que l’altitude d’un point était la distance qui le séparait verticalement du niveau de la mer. Cette définition à destination du grand public est tellement simple qu’elle semble se suffire à elle-même et ne souffrir aucune discussion. Et pourtant… Où se situe ce point de référence à Toulouse, ce fameux « niveau de la mer » en dessous de mon immeuble, construit sur la terre ferme, à environ 142 km de la mer Méditerranée et 234 km de l’océan Atlantique à vol d’oiseau ? Sur une sphère imaginaire, centrée sur le centre de la Terre et dont la surface correspond au niveau moyen de la mer autour du globe, me direz-vous. L’affaire est un tantinet plus complexe et je vais vous présenter ce que j’en ai compris.

Si vous connaissez bien le sujet et découvrez dans cet article des erreurs ou des simplifications outrancières, n’hésitez pas à m’en faire part. Je serai heureux de parfaire ma compréhension du sujet.

50 mètres de différence…

Retour en juillet 2025. Après treize ans de bons services, mon terminal GPS Garmin eTrex 30 vient de rendre l’âme. Plutôt que d’acheter un nouveau terminal GPS doté d’un écran minuscule, je décide de donner une seconde vie à mon ancien smartphone, un Samsung J7¹. Il me faut un outil pour enregistrer les traces. J’opte pour l’application libre GPS Logger de Basic Air Data. Solution en main, je pars faire le tour de mon quartier pour réaliser un premier test.

Ce test m’a valu plusieurs surprises². La plus grosse, celle qui motive cet article six mois plus tard (je suis long à la détente), a été l’altitude du parking de mon immeuble annoncée par GPS Logger. Elle était de 200 m. Or, j’avais déjà évalué cette altitude à plusieurs reprises avec mon eTrex 30, en le posant toujours au même endroit, et en lançant une acquisition longue. Il la donnait entre 143 et 148 m. De son côté, le site Géoportail indique que ce point a pour altitude 150,09 m³. Je sais que le modèle numérique de terrain du Géoportail est bien plus précis que mon GPS. L’altitude « normale » de ce point est donc bien de 150 m et l’estimation fournie par l’eTrex 30 est plutôt correcte, sachant que le calcul d’altitude est, par nature, le point faible des GPS. Pourquoi le Samsung J7 se révélait-il aussi mauvais dans l’estimation de l’altitude, alors qu’il s’avérait plutôt précis sur les longitudes et latitudes ? En analysant les données, j’ai réalisé que cette surestimation de 50 m semblait constante sur l’intégralité du parcours. L’erreur n’était donc pas imputable à un problème de réception du signal à proximité de mon immeuble. J’ai constaté la même erreur à l’issue d’une seconde balade, sur un autre itinéraire. J’en ai déduit que la puce ou l’antenne GPS du Samsung J7 étaient de piètre qualité et j’ai décidé d’acheter un autre smartphone d’occasion.

Pour faire le bon choix, j’ai demandé conseil à la communauté OpenStreetMap sur le forum francophone en expliquant le problème que je venais de rencontrer. En lisant les réactions, j’ai découvert une complexité que je ne soupçonnais pas.

De la sphère au géoïde

Pour commencer, seule chose que je savais, la Terre n’est pas vraiment sphérique. Sa rotation engendre sa déformation. Elle s’aplatit légèrement aux pôles et s’élargit au niveau de l’équateur. Alors que le rayon équatorial de la Terre est de 6 378,14 km, son rayon polaire n’est que de 6 356,75 km (21,39 km de moins). Cette forme légèrement aplatie se nomme un ellipsoïde de révolution. D’aucuns me diront que je tétracapillosectomise, que je parle là d’une déformation de 0,34 %. Certes, la forme de la Terre n’a rien de la soucoupe volante⁴. Mais 21,39 km, c’est 4,5 fois l’altitude du Mont Blanc (4 806 m) et 2,4 fois celle de l’Everest (8 849 m). Donc, 21,39 km, cela compte quand on parle d’altitude.

Cet ellipsoïde de révolution de la Terre est l’ellipsoïde de référence (IAG GRS 80 pour les intimes) du système géodésique WGS 84 utilisé par le GPS et, plus globalement, par tous les systèmes spatiaux. Les coordonnées qu’il fournit – longitude, latitude et altitude – se réfèrent à cet ellipsoïde. L’altitude indiquée par un GPS est donc la distance⁵ qui sépare le point considéré de la surface de l’ellipsoïde. Là, on pourrait croire que l’affaire est pliée, que ce n’était finalement pas si compliqué.

Que nenni ! Rappelez-vous : ce que les géographes appellent l’altitude d’un point est sa distance par rapport au niveau moyen de la mer. Or, ce fameux niveau moyen de la mer ne se confond pas en tout point avec l’ellipsoïde de référence IAG GRS 80, ni avec aucun autre ellipsoïde. Il suit approximativement⁶ une surface équipotentielle du champ de gravité terrestre, autrement dit, une surface sur laquelle la pesanteur est constante en tout point. Cette surface n’est pas régulière. Le champ de pesanteur de la Terre connait de nombreuses irrégularités du fait de la répartition hétérogène des masses constituant notre planète. Ainsi, selon l’endroit où on se trouve sur Terre, cette surface équipotentielle oscille entre 106 m en dessous (dans l’océan Indien, juste au sud de l’Inde) et 86 m au-dessus (en Islande) de l’ellipsoïde de référence. Cette surface irrégulière est appelée géoïde. À Toulouse, le géoïde se situe à 49,45 m au-dessus de l’ellipsoïde de référence. Cette différence explique pourquoi la puce GPS de mon smartphone estime l’altitude du parking de mon immeuble à 200 m alors que l’IGN l’annonce à 150 m. Eurêka !

Peut-on corriger l’estimation d’altitude ?

Cet écart constaté sur mon smartphone n’existait pas sur l’eTrex 30. Il est donc possible de le corriger dynamiquement.

En effet. La National Geospatial-Intelligence Agency (NGA) publie en libre accès des « cartes » de correction à appliquer pour obtenir l’altitude orthométrique (celle des géographes) à partir de l’altitude géométrique (celle du GPS). Ces cartes résultent de modèles gravitationnels de la Terre :

• L’EGM96 (Earth Gravitational Model publié en 1996), dont la résolution spatiale est de 15 minutes d’arc (15’), soit un carré d’environ 20 km de côté à la latitude de Toulouse.

• Le modèle EGM2008, publié en 2008 (sic !), a une résolution et une précision accrues. Sa pleine résolution est d’une minute d’arc (1’), mais on le trouve aussi en versions 2,5 minutes d’arc (2,5’) et 5 minutes d’arc (5’), ce qui donne respectivement des carrés de 1,3, 3,4 et 6,7 km de côté.

• Un modèle encore plus précis était annoncé pour 2020. Nous l’attendons encore en ce mois de janvier 2026.

Voici la « carte de chaleur » montrant l’écart d’altitude entre l’ellipsoïde et le geoïde selon le modèle gravitationnel EGM96 (image versée dans le domaine public par le Centre de vol spatial Goddard de la NASA et récupérée sur Wikimedia Commons) :

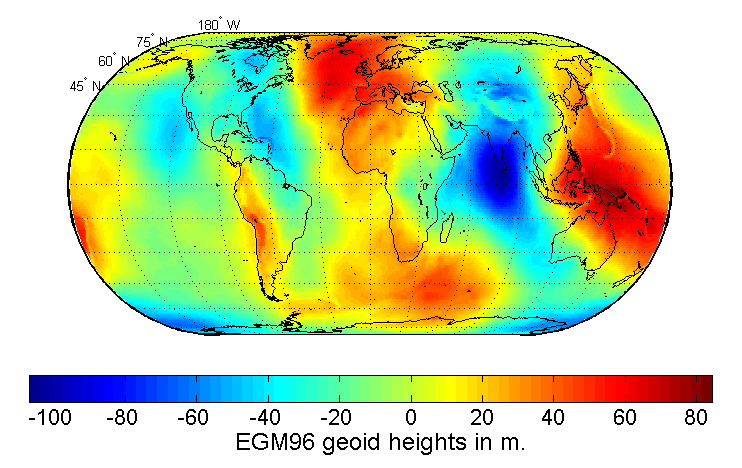
Le modèle EGM96 est le plus utilisé dans le domaine civil. Il est léger – donc facile à embarquer et à traiter – et, si les modèles ultérieurs sont plus précis, l’EGM96 suffit à corriger l’altitude de manière satisfaisante au regard de l’usage grand public du GPS. Prenons l’exemple de la correction d’altitude chez moi. L’EGM96 annonce une correction de 49,1 m, alors que l’EGM2008 en annonce une de 49,45 m. Cette différence de 35 cm est largement inférieure à la précision altimétrique d’un GPS grand public. Mais elle est énorme pour un géomètre utilisant un GPS différentiel qui certifie l’altitude à 2 cm près. Le fichier EGM96 au format PGM (portable graymap) a une taille de seulement 2 Mo quand celui de l’EGM2008 a une taille de 445 Mo dans sa résolution maximale. Chacun choisira donc son modèle en fonction de son besoin et de son équipement.

En France, l’Institut national de l’information géographique et forestière (IGN) a choisi un autre ellipsoïde, plus représentatif sur notre territoire, et il publie sa propre carte de correction (ou conversion) d’altitude, appelée RAF20 (pour la France métropolitaine). J’ignore comment je pourrais les exploiter dans les logiciels que j’utilise et si cela ferait sens. Disposer d’un modèle un peu moins précis en France, mais fonctionnant partout à travers la planète, me semble plus judicieux au regard de mon usage.

Correction d’altitude dans les applications mobiles

J’utilise quatre applications susceptibles d’afficher et d’enregistrer ma géolocalisation :

• OsmAnd
• Comaps
• GPS Logger (celle du projet Basic Air Data)
• OpenTracks

OsmAnd n’effectue aucune correction d’altitude par défaut. Il est possible d’y remédier en téléchargeant la carte « Monde - Correction d’altitude », comme cela est expliqué dans la section Altitude: Current Location de la documentation.

Comaps n’effectue aucune correction d’altitude et je n’ai pas trouvé le moyen d’y remédier.

GPS Logger n’effectue aucune correction d’altitude par défaut. Il est possible d’y remédier en activant l’option « Correction EGM96 » dans les paramètres de l’application. Elle télécharge alors d’elle-même le fichier correspondant. Si cela ne fonctionne pas, il est possible de le faire manuellement, comme les auteurs l’expliquent sur la page Manual Setup of the EGM Altitude Correction.

OpenTracks intègre nativement une correction d’altitude basée sur le modèle EGM2008.

Vous le voyez, la situation est loin d’être homogène et il faut l’étudier au cas par cas. Quoi qu’il en soit, je sais maintenant que l’altitude orthométrique de mon parking est bien de 150 m. Me voilà rassuré. :)

Quant à vous, si vous souffrez d’insomnie, vous pouvez maintenant raffiner ce questionnement en vous demandant ce qu’on appelle la verticale. Là encore, tout est affaire de référence et les coordonnées géographiques d’un point en dépendent.